This is something you likely have some intuition about. Consider the following:
- A poll shows some politician leading by a higher margin than earlier polls. What do you expect the next poll to show?
- A financial instrument dropped 10% today. What do you expect it might do tomorrow?
- A woman wins a nobel prize. Where do you expect her children's science careers to peak?
If your intuition is the same as mine, in these cases you'd expect the first part to be an outlier, and the second part to "revert to the mean", i.e. not be an extreme outlier as well.
Turns out this intuition can be backed by something you might call "a law of statistics", which was discovered by Sir Francis Galton1. Galton noticed that children's heights were correlated with their parents' (and thus came up with the term "co-related"). He noticed that tall parents have tall kids, and wondered why the overall distribution in the population remained constant. That is, if tall parents have been having tall children for generations, where are the 7-foot humans today? In his paper in the 1886 Journal of the Anthropological Institute2, he produced this oldschool figure:
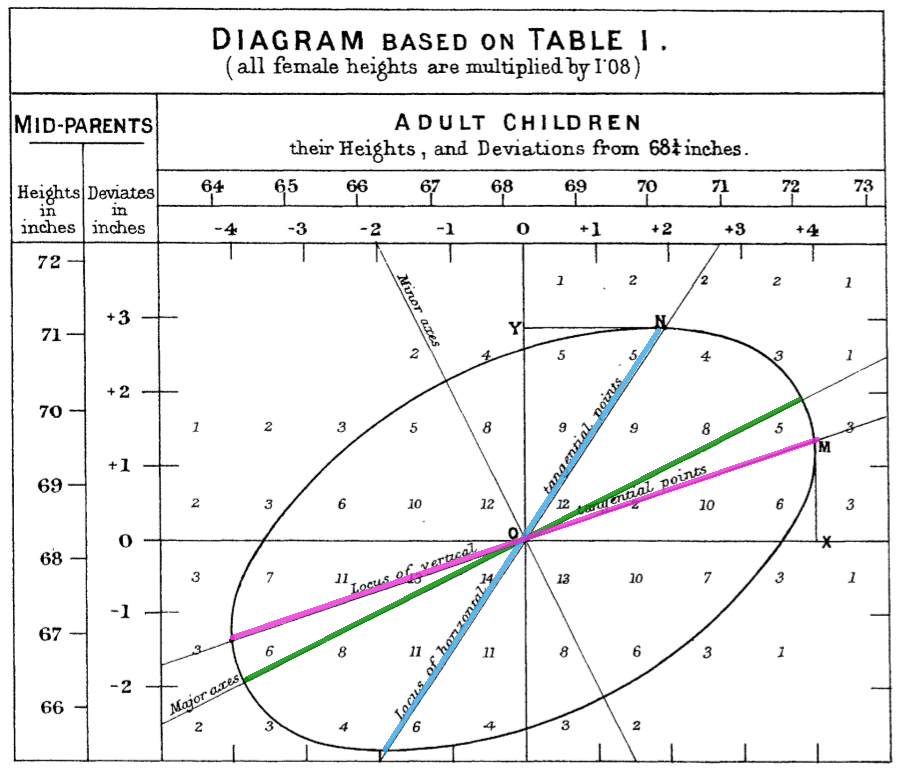
The x-axis has children's heights, and the y-axis the heights of parents. The ellipse shows the familiar shape of a bivariate normal distribution. The green line is the axis of symmetry ($x=y$), and the pink line is the regression line ($x=ay$).
The important observation: The slope of the regression line regressing children's height on their parents', is less than 1. If it were larger than 1, then very tall parents would have very-taller children generation after generation, and the distribution would widen out. The coefficient being less than 1, this is where regression to the mean happens.
So while tall parents have taller-than-average children, those children still likely to be less tall than their tall parent. While a politician who polls extremely high is likely to poll high in the following polls, she's not likely to poll quite as high next time. And whenever a parent is an extreme outlier in any sense, be it height or number of nobel prizes won, their children are likely to be less extreme in that same respect, that is, revert to the mean.